INTRODUCTION OF DIGITAL LOGIC

Digital logic is the fundamental concept underpinning all modern computer systems. Put simply, it’s the system of rules that allow us to make extremely complicated decisions based on relatively simple “yes/no” questions.

·      COMBINATIONAL LOGIC

1)       A logic block contains no memory and computes the output given the current inputs.

2)       Can be defined in three ways:

a)       Truth Table – the truth table shows many possible combination of input values, in tabular from between the input values and the result of a specific Boolean operator or combinations on the input variables.

b)       Graphical Symbols – the layout of connected gates that represent the logic circuit

a)       Boolean Equation – Boolean function that consist possible combination of inputs that produce an output signal

(1)     Examples:

·      BOOLEAN QUATION FORM

A Boolean algebra is the combination of variables and operators. Typically it has one or more inputs and produces an output in the range of 0 – 1. The complement of a variable is shown by a bar over the letter.

All Boolean equation can be represented in two forms:

1)   Sum-of-product (SOP)

a)   Combination of input values that produces 1s is convert into equivalent variables, AND-ed together then OR-ed together with others combination variables with the same output.

SOP is easier to derived from truth table.

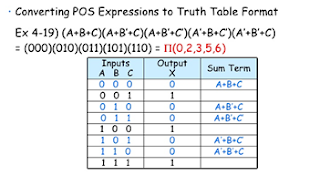
1)   Product-of-sum (POS)

a)   Input combination that produces 0s in sum terms ( OR-ed variables) are AND-ed together.

b)   Convert input that produces 0s into equivalent variables, OR-ed variables, then AND-ed with other OR-ed variables.

·     SIMPLIFICATION OF BOOLEAN EQUATION

There are two ways to simplify Boolean equation, Laws of Boolean Algebra and Karnaugh Map.

·        Laws of Boolean Algebra – rules to simplify Boolean expression

·        Karnaugh Map – A grid-like representation of a truth table

·      Laws of Boolean Algebra

Boolean expressions can be simplified or manipulated. Table below shows the basic rules of Boolean Algebra to help manipulating logic equations.

·      Karnaugh Map

The Karnaugh map provides a simple and straight forward method of minimizing Boolean expressions. The only limitation is that it will be ineffective for more than 4 inputs.

The Karnaugh map can also be describe as a grid like representation of a truth table. The rows and columns corresponds to the possible values of the function inputs.

A product term that includes all of the variables once, either complimented or not complemented is called a minterm. For example, if there are two input values A and B, there are four minterms A’B’, A’B , AB’, AB, which represent all of the possible input combinations for the function.

EXAMPLE OF MINTERMS

Karnaugh map can be applied to expressions of more than two variables. We simply extend Karnaugh map for two variables to three variables as indicated in the above figure.

·      GROUPING 1’S IN KARNAUGH MAP

a)     The group can only contain 1s.

b)     Only 1s adjacent cells can be grouped; diagonal grouping is not allowed.

c)     The number of 1s in a group must be a power of 2, means a group can contain 2,4,8,16 of 1s.

d)     The group must be as large as possible while still following all rules.

e)     All 1s must belong to a group, even if it is a group of one.

f)       Overlapping groups are not allowed

g)     Use the fewest number of groups possible

·      SIMPLIFIED EQUATION TO LOGIC CIRCUIT

                                I.            A SYMBIOSIS PROCESS: for every Boolean expression there is a logic circuit, and for every logic circuit there is a Boolean expression.in other words, we can derive the other if we have one of them.

                             II.            Simplifien L2 is represented into logic circuit

                           III.            From the L2 equation the SOP equation is the input for L2 (output). There are 3 inputs s1,s2, and s3 where 2 input will be AND-ed and OR-ed with 2 AND gates.

                          IV.            If any other 2 AND gate variables such as AB + A’C,we still use 3 inputs,A,B and C as A’ can be represented using an inverted A.

                             V.            Figure below shows the logic circuit that represent L2 function

·      UNIVERSAL GATES

Gates that can be used to implement any gates ;ike AND, OR and NOTor any combination  of these basic gates are called universal gates. NAND and NOR are such examples.

                 I.            NAND GATE

A NAND gate is a logic gate which produce an output that false only if all of its inputs are true. Figure below shows the truth tableand graphical symbol of NAND gate.

                 I.            NOR GATE

A NOR gate is a logic gate which produces a high output (1) results if both the inputs to the gate are LOW(0); a LOW output (0) results if are both inputs is HIGH (1). Figure below shows the truth table and graphical symbol for NOR gate.